科二考试系统-矩阵

2021-07-13

在上篇文章中，遗留一个问题：世界坐标系里的坐标，假设 Pos(1000,1000) 这个点即是相对原点往北 10 米，往东 10 米的一个点，而安卓原点在左上角，如何将这个点绘制在安卓屏幕上呢？
其实很简单：直接画。
假设屏幕像素为1920*1080，简单一点让地图 MapView 的宽高也是这个，那么这个点就会在屏幕 (1000,1000) 的位置被绘制出来。世界坐标系中的其他所有的点，也都可以这样直接绘制。只是这样绘制之后，某些点可能在 MapView 上看不到而已，但是所有点的相对位置都是对的。接下来就要祭出大杀器「Matrix」了。

数学中的 Matrix

矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合，元素是实数的矩阵称为实矩阵，元素是复数的矩阵称为复矩阵。而行数与列数都等于 n 的矩阵称为 n 阶矩阵或 n 阶方阵。

由 m × n 个数 aij 排成的 m 行 n 列的数表称为 m 行 n 列的矩阵，简称 m × n 矩阵。记作：

矩阵有加法：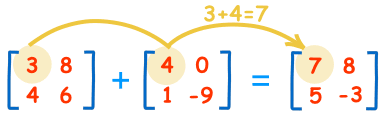

有减法：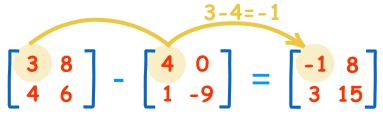

也可以进行转置：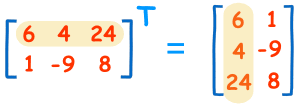

最后还有…乘法。
乘以常数：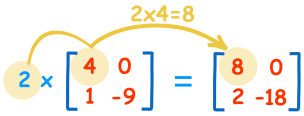

若乘以矩阵，我们要计算行与列的「点积」。
第一步：

第二步：

最后一步：

矩阵的乘法，在生活中也有实际的运用。
假设一家饼店，各类饼的价格如下：

牛肉派卖￥3一个
鸡肉派卖￥4一个
素菜派卖￥2一个
过去 4 天卖饼的数目：

如果要得出星期一的销售额：牛肉派的销售额 + 鸡肉派的销售额 + 素菜派的销售额 -> $3×13 + $4×8 + $2×6 = $83。
最终我们可以得到这样的矩阵运算：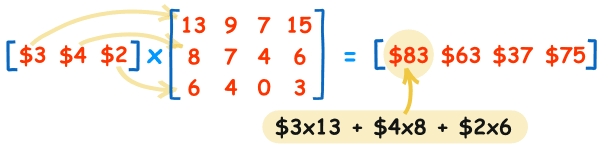

如果要统计 4 天的销售额，将结果累加即可。

乘法有了，那除法呢？实际上并不会使用除法，而是使用逆矩阵进行乘法。

A/B = A × (1/B) = A × B-1
其中 B-1 是 B 的 “逆矩阵”。

矩阵与其逆矩阵相乘，结果是单位矩阵 I：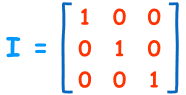

基本概念了解结束，做下小结：

只有对于两个行数、列数分别相等的矩阵（即同型矩阵），加减法运算才有意义，即加减运算是可行的。加减法满足交换律与结合律；
矩阵与数的乘法满足结合律和分配律；
矩阵与矩阵的乘法，必须满足一个条件：左矩阵的列数＝右矩阵的行数。1 × 3 的矩阵乘以 3 × 1 的矩阵，结果是 3 × 3 的矩阵，如果反过来则是 1 × 1 的矩阵了，可见矩阵的乘法不满足交换律;
单位矩阵是一个特殊的矩阵，对角线全是1，其他全是0。

安卓中的 Matrix

简单在代码中创建一个矩阵，打印出来是这样的：

1	Matrix{[1.0, 0.0, 0.0][0.0, 1.0, 0.0][0.0, 0.0, 1.0]}

可以发现，安卓中的默认 Matrix 是一个 3 × 3 的单位矩阵。它各行各列的作用是这样的：

第三行的 MPERSP 参数主要在 3D 效果中运用，通常为 [0.0, 0.0, 1.0]，本文不做讲解。
安卓矩阵提供四种基本的变换：

Translate：平移变换
Rotate：旋转变换
Scale：缩放变换
Skew：错切变换
关于这四类基本变换，可以参考Android中图像变换Matrix的原理、代码验证和应用。

你可能注意到了，我们坐标多了一个 1，这是使用了齐次坐标系的缘故，在数学中我们的点和向量都是这样表示的(x, y)，两者看起来一样，计算机无法区分，为此让计算机也可以区分它们，增加了一个标志位，增加之后看起来是这样:
(x, y, 1) - 点
(x, y, 0) - 向量

然后再来看看 Matrix 提供的方法：

这里重点说下，pre 和 post，一个是左乘，一个是右乘，根据前面所说，矩阵的乘法是不具备交换律的，所以一定要注意调用的方法及顺序。

最后

最后回到开头，世界坐标系其实并不需要映射，直接绘制在安卓界面上即可。只不过矩阵默认 scale = 1，translate = 0，就会导致一些点不在界面的可见范围内。但是地图肯定是支持拖动以及缩放的，那么识别具体的手势动作，设置相应的 Matrix 即可进行变换了。在初始化时针对坐标、MapView 的大小，以及原点计算一个缩放比例，调用 postScale 方法即可，可以指定以哪个点进行缩放：

/**
 * Postconcats the matrix with the specified scale. M' = S(sx, sy, px, py) * M
 */
public boolean postScale(float sx, float sy, float px, float py) {
    nPostScale(native_instance, sx, sy, px, py);
    return true;
}

设置矩阵转化前：

设置矩阵转化后：

数学中的 Matrix

安卓中的 Matrix

最后

参考